Lecture 13 Nov 2001, Per Kraulis
It turns out that sequence profiles are a special case of a more general mathematical approach, called hidden Markov models (HMMs). These methods were originally used in speech recognition before the were applied to biological sequence analysis. A well-defined formalism exists, which helps with the theoretical understanding of what can be expected when applying it to sequence analysis. This is an important advantage of using HMMs instead of sequence profiles; the underlying theoretical basis is much more solid. Also, Bayesian statistics is used in several aspects of the method.
A Markov process is a physical process of a special, but common kind. The basic idea is that we have a physical system that stepwise goes through some kind of change. For example, it may be die (svenska: "tärning") that we throw time and again; the change is the transition from the new value to the next. An essential characteristic of a Markov process is that the change is dependent only on the current state. The history of the system does not matter. The states that the system has been in before are not relevant, only the current state determines what will happen next. The system has no memory.
One may view a protein (or DNA) sequence as the record of such a process. There is some hidden process that generates a sequence of amino-acid residues, where chance (based on specific probabilities) play an essential role in determining the exact sequence being produced. This is one (very crude) way of describing an HMM.
This approach can be applied in sequence motif searches. Given a multiple sequence alignment of a particular domain family, one uses statistical methods to build a specific HMM for that domain family. The probabilities that are required are estimated from the frequencies in the alignment, together with other data. This HMM can then be used to test other sequences whether they match this domain family or not. HMMs can be set up so that insertions, deletions and substitutions can be handled in sensible ways, and their probabilities estimated properly.
The plan (or topology) of an HMM determines which probabilities need to be estimated, and what kind of matches are allowed. For instance, it is perfectly possible to design an HMM plan that strictly forbids insertions and deletions. This means that it is very important for the HMM designer (i.e. the software programmer, usually not the user) to decide on which type of topology that should be implemented. This will determine which kinds of sequence profiles that can be matched by the HMM.
In an HMM plan designed for matching a sequence, each state corresponds to a residue in the sequence. The transitions between the states are assigned probabilities that are determined from the multiple sequence alignment that is used as training set. In order to test whether a new sequence contains a segment that matches the HMM profile, an algorithm that works essentially like a dynamical programming algorithm is used to find the best match between the HMM profile and the sequence. The best match is the one that maximizes the transition probabilites given those particular residues.
Here is an example of what an HMM plan may look like. This is the plan used in the popular HMMER software, and the image was taken from its documentation.
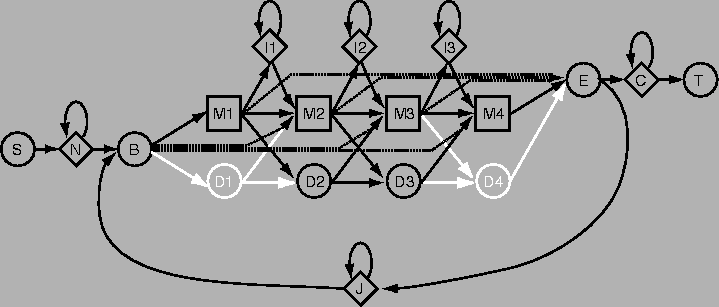
The abbreviations for the states are as follows:
Compared with the HMM plan shown in the course book (page 160). this is slightly more complicated. The reason is that the creator of HMMER (Sean Eddy) wanted to obtain a method that could locate a domain in a sequence where the true domain is flanked by possibly very large regions of non-matching sequence. Therefore the states N and C were added, which will be used to match such completely irrelevant parts of a sequence.