Om reduktionism: En glimt i ögat, del 2

I den första delen av denna artikeln visade jag en tabell av 3-ställiga siffror, och avslöjade att den var en liten bild om 9 gånger 9 pixlar. Här är bilden förstorad 10 gånger:

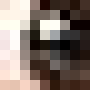
Nu ser vi litet mer. Det finns sammanhängande fält av färg, och om vi har riktigt bra fantasi kan vi möjligen gissa vad bilden föreställer. Tips: det har med rubriken på denna artikeln att göra.

Den fråga jag ställer mig är följande: Innehåller tabellen av siffror denna bilden? Existerar bilden i och med att vi specificerar tabellen? Jag skulle vilja påstå att tabellen endast är en representation av bilden; den är inte bilden i sig självt. Detta påståendet är möjligen trivialt; självklart är tabellen inte identisk med bilden!

Men säger inte den filosofiska reduktionismen just att bilden egentligen bara är ett antal färgpixlar, vars färger helt och fullt bestäms av RGB-triplarna? Bilden kan helt reduceras till siffror, och därför finns endast tabellen. Det skorrar illa gentemot det synbarligen triviala påståendet i förra stycket! Trots att all information i bilden finns i tabellen, så är bild och tabell inte samma sak. Nu hoppas jag att jag sått ett frö av tvivel hos läsaren...

När man reducerar ett fenomen till en underliggande nivå, förklarar den, så försvinner inte det ursprungliga fenomenet. Det finns kvar. Reduktionen innebär inte att illusionen avslöjas i så måtto att den inte längre syns. Vår uppfattning av verkligheten, av bilden i detta fall, får så att säga bara ett annat djup.

Låt oss, som nämndes i första delen, betrakta reduktionismen omvänt, alltså som en fråga om hur vi syntetiserar den övre nivån från den lägre. Jag vill påstå att reduktionismens intellektuella attraktionskraft är beroende av att vi redan vet vad svaret, helheten, skall vara. Givet helheten kan vi undersöka de lägre nivåerna för att förstå hur de manifesterar sig i den högre.

Och däri ligger ett problem för den filosofiska reduktionismen. Dess attraktiva drag ligger nämligen i förklaringsförmågan, att givet det högre fenomenet, använda det lägre som förklaring. Det omvända förhållandet, att givet det lägre förutse hur det högre bör se ut, är inte alls lika attraktivt, helt enkelt därför att vi intuitivt inser hur svårt det är.

Vi har ännu inte fått svaret på vad dessa 9x9 pixlar lilla bilden egentligen föreställer. Även om läsare till äventyrs kan gissa vad det är, så tror jag det är omöjligt att inse hur hela bilden ser ut.

Där har vi, tror jag, ännu ett problem med den filosofiska reduktionismen. Det finns alltid en kontext. Ibland kan den abstraheras bort, eller anses självklar. Eller, som i detta fallet, är den nödvändig för att alls förstå vad som pågår.

Låt oss gå till den sista delen av artikeln för att beskåda hela bilden.